Knapsack

背包问题 (Knapsack)

问题描述

0-1背包问题是非常经典的动态规划问题, 简单描述下这个问题, 首先你有容量为 W 的背包, 有 N 个物品可以选择装入或不装入背包, 每个物品有自己的价值和大小, 你所做的事就是在背包容量的限制下, 选择装入的物品以获得最高的利益。

求解思路

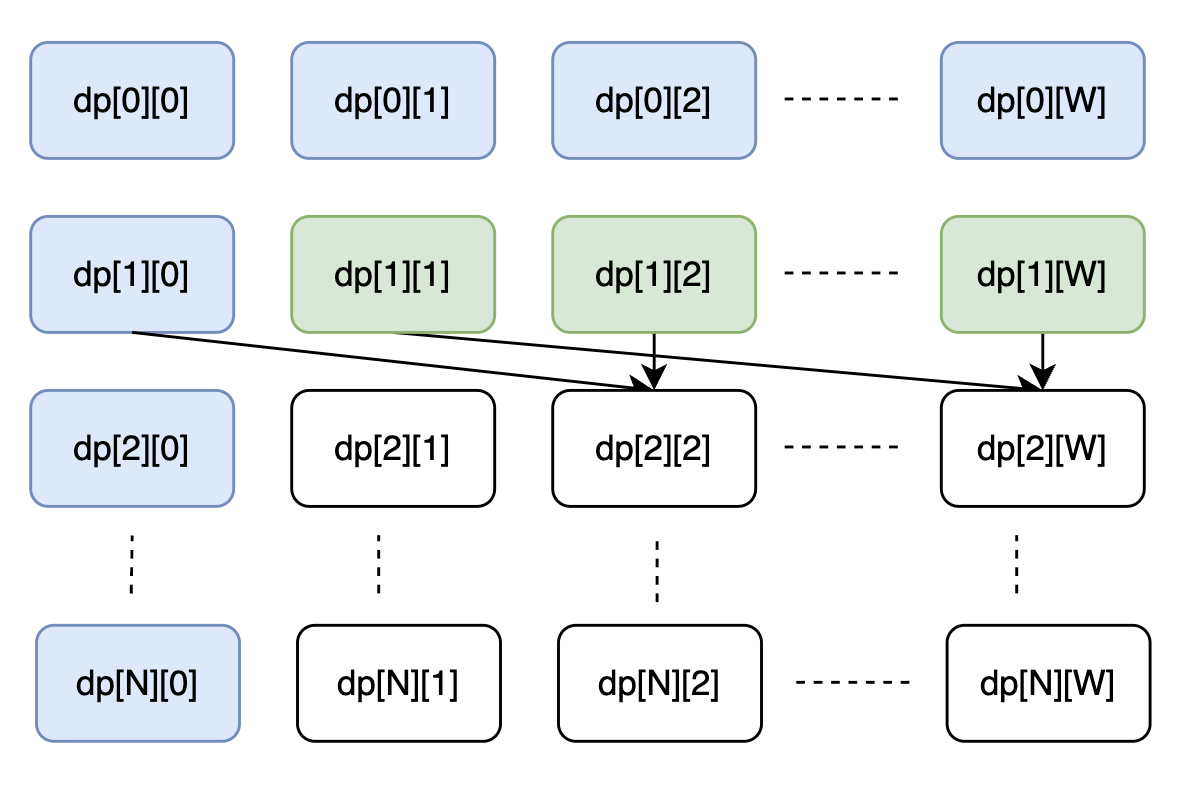
设有二维数组 dp[0..N][0..W], 其中 dp[i][j] 表示在考虑前 i 个物品并且背包容量为 j 的情况下, 可以获得的最大利益。

考虑是否装入第 i 个物品, 如果装入(当然前提是能装入), 那么获得的最大利益就是 dp[i-1][j - w[i]] + v[i], 其中 w[i] 与 v[i] 分别表示第 i 个物品的体积和价值; 如果不装入, 那么获得的最大利益就是 dp[i-1][j], 两者取最大就是 dp[i][j]。

\[dp[i][j] = \begin{cases} max(dp[i-1][j-w[i]] + v[i], dp[i-1][j]), & \text{if } j \geq w[i]\\ dp[i-1][j], & \text{otherwise} \end{cases}\]

优化 & 加速

很容易可以写出下面的代码解决背包问题, 完整的代码在 knapsack0。

int knapsack(int W, const std::vector<int> &w, const std::vector<int> &v) {
  int N = w.size();
  std::vector<std::vector<int>> dp(N + 1, std::vector<int>(W + 1, 0));
  for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= W; j++) {
      if (j < w[i - 1]) {
        dp[i][j] = dp[i - 1][j];
      } else {
        dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
      }
    }
  }
  return dp[N][W];
}

降维

我们可以对dp数组降维, 核心代码如下, 完整的代码在 knapsack1。

int knapsack(int W, const std::vector<int> &w, const std::vector<int> &v) {
  int N = w.size();
  std::vector<int> dp(W + 1);
  for (int i = 0; i < N; i++) {
    for (int j = W; j >= w[i]; j--) {
        dp[j] = std::max(dp[j], dp[j - w[i]] + v[i]);
    }
  }
  return dp[W];
}

多线程

很简单的思路, 让多个线程计算同一行 dp[i][1..W], 但是由于每个线程计算 dp[i][j] 的顺序完全随机, 所以不能够简单地降成一维, 我们必须要保留前一行的数据。核心代码如下, 完整的代码在 knapsack2。

int knapsack(int W, const std::vector<int> &w, const std::vector<int> &v) {
  int N = w.size();
  std::vector<int> dp0(W + 1);
  std::vector<int> dp1(W + 1);
  for (int i = 0; i < N; i++) {
    #pragma omp parallel for
    for (int j = W; j >= w[i]; j--) {
      dp1[j] = std::max(dp0[j], dp0[j - w[i]] + v[i]);
    }

    #pragma omp parallel for
    for (int j = 0; j < w[i]; j++) {
      dp1[j] = dp0[j];
    }

    dp0.swap(dp1);
  }
  return dp0[W];
}

源代码清单

knapsack0

#include <cstdio>
#include <vector>

int knapsack(int W, const std::vector<int> &w, const std::vector<int> &v) {
  int N = w.size();
  std::vector<std::vector<int>> dp(N + 1, std::vector<int>(W + 1, 0));
  for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= W; j++) {
      if (j < w[i - 1]) {
        dp[i][j] = dp[i - 1][j];
      } else {
        dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
      }
    }
  }
  return dp[N][W];
}

int main(int argc, char *argv[]) {
  int N, W;
  scanf("%d %d", &N, &W);
  std::vector<int> w(N), v(N);
  for (int i = 0; i < N; i++) {
    scanf("%d %d", &w[i], &v[i]);
  }
  printf("%d\n", knapsack(W, w, v));
  return 0;
}

knapsack1

#include <cstdio>
#include <vector>

int knapsack(int W, const std::vector<int> &w, const std::vector<int> &v) {
  int N = w.size();
  std::vector<int> dp(W + 1);
  for (int i = 0; i < N; i++) {
    for (int j = W; j >= w[i]; j--) {
      dp[j] = std::max(dp[j], dp[j - w[i]] + v[i]);
    }
  }
  return dp[W];
}

int main(int argc, char *argv[]) {
  int N, W;
  scanf("%d %d", &N, &W);
  std::vector<int> w(N), v(N);
  for (int i = 0; i < N; i++) {
    scanf("%d %d", &w[i], &v[i]);
  }
  printf("%d\n", knapsack(W, w, v));
  return 0;
}

knapsack2

#include <cstdio>
#include <omp.h>
#include <vector>

int knapsack(int W, const std::vector<int> &w, const std::vector<int> &v) {
  int N = w.size();
  std::vector<int> dp0(W + 1);
  std::vector<int> dp1(W + 1);
  for (int i = 0; i < N; i++) {
    #pragma omp parallel for
    for (int j = W; j >= w[i]; j--) {
      dp1[j] = std::max(dp0[j], dp0[j - w[i]] + v[i]);
    }

    #pragma omp parallel for
    for (int j = 0; j < w[i]; j++) {
      dp1[j] = dp0[j];
    }

    dp0.swap(dp1);
  }
  return dp0[W];
}

int main(int argc, char *argv[]) {
  int N, W;
  scanf("%d %d", &N, &W);
  std::vector<int> w(N), v(N);
  for (int i = 0; i < N; i++) {
    scanf("%d %d", &w[i], &v[i]);
  }
  printf("%d\n", knapsack(W, w, v));
  return 0;
}